hot100刷题记录

First Post:

Last Update:

二分

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
int searchInsert(vector<int>& nums, int target) {
int n = nums.size();
int left = 0;
int right = n;
int mid = 0;

while(left<right){
	mid = left+(right-left)>>1;
	if(target<nums[mid]){
		right = mid;
	}else if(target>nums[mid]){
		left = mid+1;
	}else return mid;
}
return right;
}
};

评价：板子，多背。

74. 搜索二维矩阵

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class Solution {

public:
bool searchMatrix(vector<vector<int>>& matrix, int target) {
int l = 0;
int r = matrix.size();
int res =0;
while(l<r){
	int mid = l+((r-l)>>1);
	if(target>matrix[mid][0]){
		l=mid+1;
	}else if(target<matrix[mid][0]){
		r=mid;
	}else return true;
}

res = l-1;
if (res < 0 || res >= matrix.size()) {
	return false;
}

int l2=0;
int r2 =matrix[res].size();
while(l2<r2){
	int mid2 = l2+((r2-l2)>>1);
if(target>matrix[res][mid2]){
	l2=mid2+1;
}else if(target<matrix[res][mid2]){
	r2=mid2;
}else return true;
}
return false;

}
};

评价：太几把猪鼻了，在res<0里纠结了很久，以及，l是第一个大于target的行索引。

  • 循环结束时，l 和 r 会相等，且 l 是第一个大于或等于 target 的行索引。
  • 因此，res = l - 1 是最后一个小于 target 的行索引。

34. 在排序数组中查找元素的第一个和最后一个位置

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {

        int lower_bound(vector<int> &nums,int target){
            int left = -1,right=nums.size();
            while(left+1<right){
                int mid = left+(right-left)/2;
                if(nums[mid]<target){
                    left = mid;
                }else{
                    right = mid;
                }
            }
            return right;
        }

public:
    vector<int> searchRange(vector<int>& nums, int target) {

        int start = lower_bound(nums,target);
        if(start==nums.size()||nums[start]!=target)return {-1,-1};
        int end = lower_bound(nums,target+1)-1;
        return {start,end};
    }
};

评价：用0x3f的开区间写法，left right是循环不变量，left必定指向小于target的数，而right必定指向大于等于target的数

二叉树

94. 二叉树的中序遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:

    void inorder(TreeNode* root,vector<int>& res){
        if(!root){
            return;
        }
        inorder(root->left,res);
        res.push_back(root->val);
        inorder(root->right,res);
    }

    vector<int> inorderTraversal(TreeNode* root) {

    }
};

太史公曰：

中序遍历的递归实现
这道题不难写，但我还是想回到中序遍历的定义。

1
2
3
4
5
6
7
8
9
10
11
12
13
const inorderTraversal = (root) => {
const res = [];
const inorder = (root) => {
	 if (root == null) {
		 return;
	 }
	 inorder(root.left); // 先递归左子树
	 res.push(root.val); // 将当前节点值推入res
	 inorder(root.right); // 再递归右子树
 };
     inorder(root);
     return res;
 };

我之前提过，我们不能含糊地记说：“中序遍历是先访问左子树，再访问根节点，再访问右子树”。

这么描述是不准确的，容易产生误导。

事实上，无论是前、中、后序遍历，都是先访问根节点，再访问它的左子树，再访问它的右子树。

那它们之间的区别在哪里？

比如中序遍历，它是将 do something with root（处理当前节点）放在了访问完它的左子树之后。
比方说，Printf 一下节点值，就会产生「左 根 右」的打印顺序。
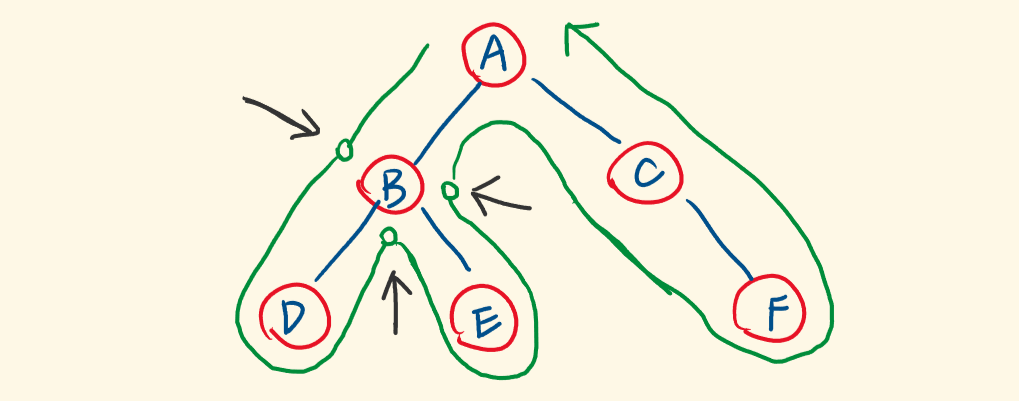
image.png

前、中、后序遍历都是基于DFS，节点的访问顺序如上图所示，每个节点有三个不同的驻留阶段，即每个节点会被经过三次：

在递归它的左子树之前。
在递归完它的左子树之后，在递归它的右子树之前。
在递归完它的右子树之后。
我们将 do something with root 这个操作，放在这三个时间点之一，就分别对应：前、中、后序遍历。

所以，它们的唯一区别是：在什么时间点去处理节点，去拿他做文章。

所以『中序遍历』的模板如下：

1
2
3
4
5
norder (root) {
    call inorder(root.left) 
    access the content of root
   call inorder(root.right)
 }

中序遍历的迭代实现
搞清楚概念后，怎么用栈去模拟递归遍历，并且是中序遍历呢？

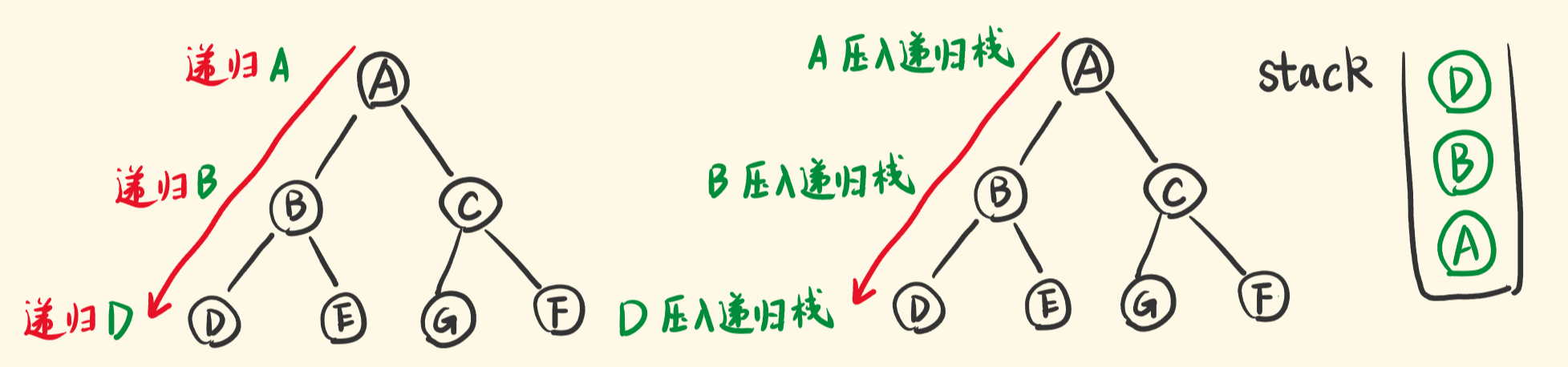
递归遍历一棵树，如下图，会先递归节点A，再递归B，再递归D，一个个压入递归栈。
image.png

即，先不断地将左节点压入栈，我们写出这部分代码：

while (root) {
stack.push(root);
root = root.left;
}
DFS的访问顺序是：根节点、左子树、右子树，现在要访问已入栈的节点的右子树了。

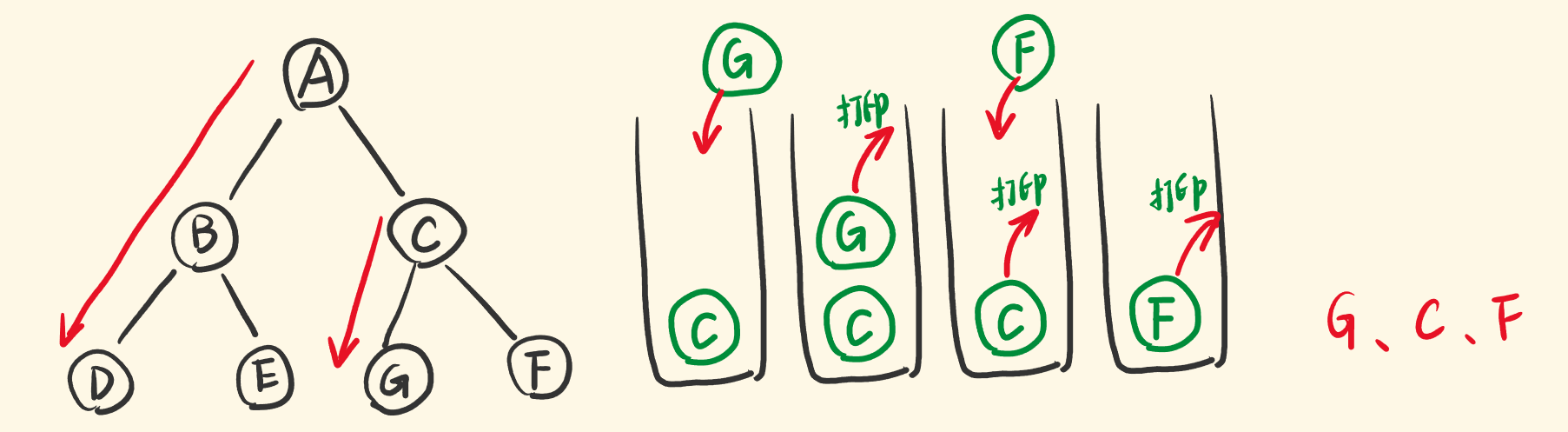
并且是先访问『位于树的底部的』即『位于栈的顶部的』节点的右子树。

于是，让栈顶节点出栈，出栈的同时，把它的右子节点压入栈，相当于递归右子节点。

因为是中序遍历，在栈顶节点的右子节点压栈之前，要处理出栈节点的节点值，将它输出。

新入栈的右子节点（右子树），就是在递归它。和节点A、B、D的压栈一样，它们都是子树。

不同的子树要做同样的事情，一样要先将它的左子节点不断压栈，然后再出栈，带出右子节点入栈。
image.png

即栈顶出栈的过程，也要包含下面代码，可见下面代码重复了两次：

while (root) {
stack.push(root);
root = root.left;
}
其实这两个 while 循环，分别对应了下面的两次 inorder 调用，就是递归压栈：

inorder(root.left);
res.push(root.val);
inorder(root.right);
迭代实现 代码
js
go
const inorderTraversal = (root) => {
const res = [];
const stack = [];

while (root) { // 能压栈的左子节点都压进来
stack.push(root);
root = root.left;
}
while (stack.length) {
let node = stack.pop(); // 栈顶的节点出栈
res.push(node.val); // 在压入右子树之前，处理它的数值部分（因为中序遍历）
node = node.right; // 获取它的右子树
while (node) { // 右子树存在，执行while循环
stack.push(node); // 压入当前root
node = node.left; // 不断压入左子节点
}
}
return res;
};
我把递归写法再次拿出来，供大家对比，感受一下二者的区别和相同点。

1
2
3
4
5
6
7
8
9
10
11
12
13
const inorderTraversal = (root) => {
  const res = [];
 const inorder = (root) => {
    if (root == null) {
      return;
    }
    inorder(root.left);
    res.push(root.val);
    inorder(root.right);
  };
  inorder(root);
  return res;
};

全流程大致图示

后记
暂且分析中序遍历，前序遍历和后序遍历的迭代版分析也许会补充上来，大家可以动手试试。

明确这三种遍历都是基于DFS递归，清楚概念，再明白递归其实是压栈出栈的操作，比照着，用一个栈，去模拟递归栈，用迭代，去模拟递归的逻辑，就不难写出迭代法的代码。

回溯

46. 全排列

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
private:
vector<vector<int>> res;
vector<int> path;
    void dfs(vector<int> nums,int x,vector<bool> used){
        if(x==nums.size()){
            res.push_back(path);
            return;
        }
        for(int i = 0;i<nums.size();i++){
            if(used[i])continue;
            used[i]=true;
            path.push_back(nums[i]);
            dfs(nums,x+1,used);
            used[i]=false;
            path.pop_back();
        }
    }
public:
    vector<vector<int>> permute(vector<int>& nums) {
        int n = nums.size();
        vector<bool> used(n);
        dfs(nums,0,used);
        return res;
    }
};

评价：循环该从0开始，每次都是遍历整个数组找没用过的数

78. 子集

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
private:
vector<vector<int>> res;
vector<int> path;
    void dfs(vector<int> nums,int x){
        res.push_back(path);
        for(int i = x;i<nums.size();i++){
            path.push_back(nums[i]);
            dfs(nums,i+1);
            path.pop_back();
        }
    }
public:
    vector<vector<int>> subsets(vector<int>& nums) {
        dfs(nums,0);
        return res;
    }
};

评价：dfs参数是i+1,避开已经看过的数

前缀和与子串

303. 区域和检索 - 数组不可变

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class NumArray {
    
public:
vector<int> s;
    NumArray(vector<int>& nums) {
        s.resize(nums.size()+1);
        s[0]=0;
        for(int i =0;i<nums.size();i++){
            s[i+1]=s[i]+nums[i];
        }
    }
    
    int sumRange(int left, int right) {
        return s[right+1]-s[left];
    }
};

/**
 * Your NumArray object will be instantiated and called as such:
 * NumArray* obj = new NumArray(nums);
 * int param_1 = obj->sumRange(left,right);
 */

560. 和为 K 的子数组

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
class Solution {
public:
    int subarraySum(vector<int>& nums, int k) {
        vector<int> s(nums.size()+1);
        unordered_map<int,int> cnt;

        s[0]=0;
        for(int i=0;i<nums.size();i++){
            s[i+1]=s[i]+nums[i];
            cnt[s[i]]++;
        }

        int ans = 0;
        for(int i =0;i<s.size();i++){
            ans += cnt[s[i]-k];
        }


        return ans;        
    }
};//这是错的 错误关键在于 遍历前缀和时应该在遍历之后在哈希表里++，下面是自己的写法和0x3f写法

//自己的正确写法
class Solution {
public:
    int subarraySum(vector<int>& nums, int k) {
        vector<int> s(nums.size()+1);
        unordered_map<int,int> cnt;

        s[0]=0;
        for(int i=0;i<nums.size();i++){
            s[i+1]=s[i]+nums[i];
        }

        int ans = 0;
        for(int i =0;i<s.size();i++){
            ans += cnt[s[i]-k];
            cnt[s[i]]++;
        }
        return ans;        
    }
};

//0x3f写法
class Solution {
public:
    int subarraySum(vector<int>& nums, int k) {
        vector<int> s(nums.size()+1);
        unordered_map<int,int> cnt;
        int ans = 0;

        for(int i=0;i<nums.size();i++){
            s[i+1]=s[i]+nums[i];
        }

        for (int i=0;i<s.size();i++) {
            // 注意不要直接 += cnt[s[i]-k]，如果 s[i]-k 不存在，会插入 s[i]-k
            ans += cnt.contains(s[i] - k) ? cnt[s[i] - k] : 0;
            cnt[s[i]]++;
        }

        return ans;        
    }
};
//1 2 3
//0 1 3 6
//0:1 1:1 3:1 3-3=0:1 3:1 6:1

239. 滑动窗口最大值

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
public:
    vector<int> maxSlidingWindow(vector<int>& nums, int k) {
        // for(int r =0;r<nums.size();l++){
        //     r=l+k;
        //     int a = l;
        //     int temp = -100000;
        //     while(a<r){
        //         temp = max(nums[a],temp);
        //         a++;
        //     }
        //     res.push_back(temp);
        // }
        // return res;

        vector<int> res;
        int n = nums.size();
        priority_queue<pair<int,int>> p;
        for(int r = 0;r<nums.size();r++){
            p.push({nums[r],r});
            if(p.size()>=k){
                while(p.top().second<=r-k){
                    p.pop();
                }
                res.push_back(p.top().first);
            }
        }
        return res;
    }
};

image.png

≡